Perpendicular directions samples relative to a given vector#
As I mentioned in the mid-term summary, one of my next steps is to implement some numerical methods to compute the standard kurtosis measures to evaluate their analytical solution.
The numerical method for the perpendicular kurtosis requires samples of perpendicular directions to a given vector v.
I am posting here the mathematical basis of this function which will be implemented in module dipy.core.geometry and named as perpendicular_directions.
Function’s Algorithm#
- Inputs:
Vector v: Perpendicular directions are sampled relative to this vector.
N: Number of perpendicular directions
Step 1) The N directions are first sampled in the unit circumference parallel to the y-z plane (plane normal to the x-axis), as shown the figure below.
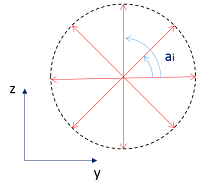
Fig 1. First step of perpendicular_directions algorithm.#
Coordinates of the perpendicular directions are therefore initialized as:

(Eq. 1)#
where ai are the angles sampled for [0, 2*pi [. To perform N samples, the angle between two adjacent directions is given by 2*pi / N.
Step 2) Sampled directions are then rotated and aligned to the plane normal to vector v (see figure below).
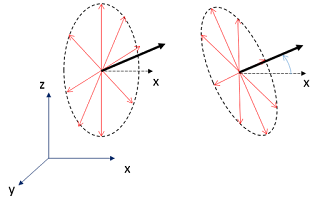
Fig 2. Second step of perpendicular_directions algorithm.#
Mathematically, this is done by multiplying each perpendicular directions ni by a rotational matrix. The final perpendicular directions di are given by:
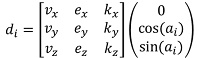
(Eq. 2)#
The rotational matrix in Eq.2 is constructed as the reference of frame basis in which the first basis axis is the vector v, while the other two basis axis are any pair of orthogonal directions pair relative to vector v. These orthogonal vectors are named here as vector e and vector k. For the implementation of function perpendicular_directions, vectors e and k are estimated using the following procedure:
The direction of e is defined as the normalized vector defined by the cross product between vector v and the unit vector aligned to x-axis, i.e [1, 0, 0]. After normalizing, the final coordinates of e are:
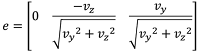
(Eq. 3)#
k is directly defined as the cross product between vectors v and e. The coordinates of this vector are:
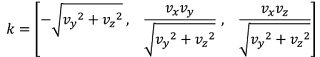
(Eq. 4)#
From equations 2, 3 and 4, the coordinates of the perpendicular directions relative to vector v are give as:
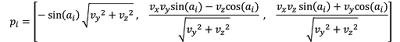
(Eq. 5)#
Note that Eq. 5 has a singularity when vector v is aligned to the x-axis. To resolve this singularity, perpendicular directions are first defined in the x-y plane and vector e is computed as the normalized vector given by the cross product between vector v and the unit vector aligned to the y-axis, i.e [0, 1, 0]. Following this, the coordinates of the perpendicular directions are given as:
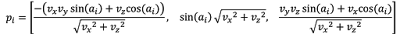
(Eq. 6)#