Progress Report on Diffusion Kurtosis Imaging (DKI) Implementation#
Progress is going as planned in my mid-term summary :).
A short summary of what was done in the last weeks is described in the points below:
The functions to fit the diffusion kurtosis tensor are already merged to the main Dipy’s repository (you can see the merged work here).
The functions to extract kurtosis statistics were submitted in a separate pull request. Great advances on the validation of these functions were done according to the next steps pointed in the mid-term summary. Particularly, I completed the comparisons between the analytical solutions with simpler numerical methods (for nice figures of these comparisons, see below the subsection “Advances on the implementation of DKI statistics”).
At the same time that I was waiting for the revision of the work done on kurtosis tensor fitting and statistic estimation, I started working on functions to estimate the direction of brain white matter fibers from diffusion kurtosis imaging. This work is happening in a new created pull request. For the mathematical framework of this implementation and some nice figures of the work done so far, you can see below the subsection “DKI based fiber estimates”.
Advances on the implementation of DKI statistics#
Improving the speed performance of functions#
As mentioned on the last points of my mid-term summary, some features on the functions for estimating kurtosis statistics to reduce the processing time were added. At the time of the mid-term evaluation, I was planning to add some optional inputs to receive a mask pointing the relevant voxels to process. However, during the last weeks, I decided that a cleaver way to avoid processing unnecessary background voxels was to create a subfunction that automatically detects these voxels (detecting where all diffusion tensor elements are zero) and exclude them. In addition, I also vectorized parts of the codes (for details on this, see directly the discussion on the relevant pull request page). Currently, reprocessing the kurtosis measures shown in Figure 1 of my post #6 is taking around:
Mean Kurtosis - 14 mins
Radial Kurtosis - 7 mins
Axial Kurtosis - 1 min
Using ipython profiling techniques, I also detected the parts of the codes that are more computationally demanding. Currently, I have been discussing with members of my mentoring organization the possibility of converting this function in cython.
Comparison between mean kurtosis analytical and approximated solutions#
Mean Kurtosis (MK) corresponds to the average of the kurtosis values along all spatial directions. Therefore, an easy way to estimate MK is to sample directional kurtosis values in evenly sampled directions and compute their average. This procedure can be very easy to implement, however it has some pitfalls as requiring a sufficient number of direction samples and being dependent on the performance of the direction sampling algorithms. Fortunately, this pitfalls can be overcome using an analytical solution that was proposed by Tabesh and colleagues.
In previous steps of my GSoC project, I had already implemented the MK estimation functions according to the analytical solution. However, I decided to implement also the directional average since it could be useful to evaluate the analytical approach. In the figure below, I run this numerical estimate for different number of directions, to analyse how many directions are required so that the directional kurtosis average approaches the analytical mean kurtosis solution.
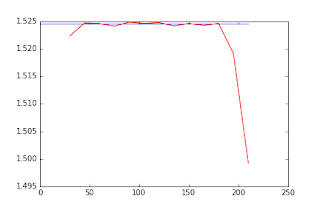
Figure 1 - Comparison between the MK analytical (blue) and numerical solutions (red). The numerical solution is computed relative to a different number of direction samples (x-axis).#
From the figure above, we can see that the numerical approach never reaches a stable solution. Particularly, large deviations are still observed even when a large number of directions is sampled. After a careful analysis, I noticed that this was caused by imperfections on the sphere dispersion algorithm strategies to sample evenly distributed directions.
Due to the poor performance, I decided to completely remove the MK numerical solution from the DKI implementation modules. This solution is only used on the code testing procedures.
Comparison between radial kurtosis analytical and approximated solutions#
Radial kurtosis corresponds to the average of the kurtosis values along the perpendicular directions of the principal axis, i.e. the direction of non-crossing fibers. Tabesh and colleagues also proposed an analytical solution for this kurtosis statistic. I implemented this solution in Dipy on my previous steps of the GSoC project. Nevertheless, based on the algorithm described in my post #8, radial kurtosis can be estimated as the average of exactly evenly perpendicular direction samples. The figure below shows the comparison between the analytical solution and the approximated solution for a different number of perpendicular direction samples.
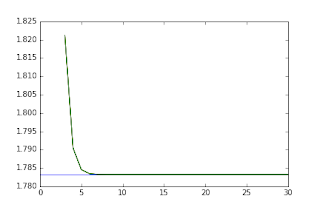
Figure 2 - Comparison between the RK analytical (blue) and numerical solutions (green). The numerical solution is computed relative to a different number of direction samples (x-axis).#
Since, opposite to the MK case, the algorithm to sample perpendicular directions does not depend on sphere dispersion algorithm strategies, the numerical method for the RK equals the exact analytical solution after a small number of sample directions.
Future directions of the DKI statistic implementation#
Having finalized the validation of the DKI statistic implementation, the last step of the DKI standard statistic implementation is to replace the data used on the sample usage script by an HCP-like dataset. As mentioned on my post #7, the reconstructions of the dataset currently used on this example seems to be corrupted by artifacts. After discussing with an expert of the NeuroImage mailing list, these artefacts seem to be caused by an insufficient SNR for fitting the diffusion kurtosis model.
DKI based fiber direction estimates#
Mathematical framework#
This fiber direction estimation is done based on the orientation distribution function as proposed by Jensen and colleagues (2014). The orientation distribution function (ODF) gives the probability that a fiber is aligned to a given direction and it can be estimated from the diffusion and kurtosis tensors using the following formula:
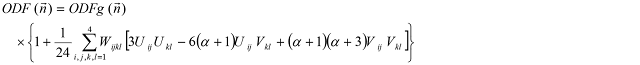
where α is the radial weighting power, Uij is the element ij of the dimensionless tensor U which is defined as the mean diffusivity times the inverse of the diffusion tensor (U = MD x iDT), Vij is defined as
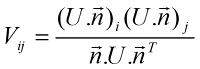
and ODFg the Gaussian ODF contribution which is given by:
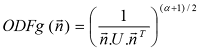
Implementation in python 1#
In python, this expression can be easily implemented using the following command lines:

(Note: For a description of what from_lower_triangular does, see Dipy’s DTI module).
Results#
In the figure below, I show a ODF example obtained from the simulation of two white matter crossing fibers.
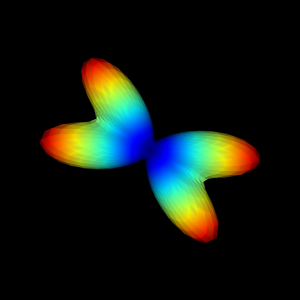
Figure 3 - DKI-ODF obtained from two simulated crossing fibers. Maxima of the ODF correspond to the direction of the crossing fibers.#
From the figure above, we can see that the ODF has two directions with maxima amplitudes which correspond to the directions where fibers are aligned.
Implementation in python 2#
The lines of codes previously presented correspond to a feasible implementation of Jensen and colleagues formula. However, for the implementation of the DKI-ODF in dipy, I decided to expand the four for loops and use kurtosis tensor symmetry to simplify this expansion. The resulting code is as follows:

This implementation of the ODF can look less optimized, but in fact it involves a smaller number of operations relative to the four for loops of the algorithm in “Implementation in python 1”. Particularly, this version of the code is more than 3 times faster!
Future directions of the DKI-ODF implementation#
An algorithm to find the maxima of the DKI-ODF will be implemented. The direction of maxima ODF will be used as the estimates of fiber direction that will be useful to obtain DKI based tractography maps (for a reminder of what is a tractography map, see my post #3).